Il paradosso di Achille e la tartaruga

 Fu Zenone di Elea, filosofo greco vissuto nel V secolo a.C., a proporre il celebre paradosso di Achille e della tartaruga.
Immaginò che Achille, noto per essere il “piè veloce”, venisse sfidato a raggiungere (non superare nella corsa) la lenta tartaruga, alla quale fu però concesso un vantaggio iniziale. Il paradosso era fondato su questo presupposto: nel tempo che Achille impiega per raggiungere il punto in cui inizialmente si trova la tartaruga , quest’ultima avrà, comunque, percorso un piccolo tratto. Quando Achille avrà percorso questo piccolo tratto, la tartaruga sarà ulteriormente avanzata. E Achille non raggiungerà mai la tartaruga, perché dovrà percorrere gli infiniti spazi che colmano la distanza tra i concorrenti.

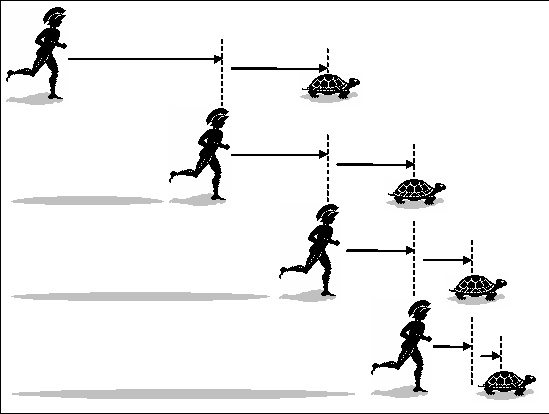
Già Aristotele diede una sua definizione del paradosso sostenendo che “un mobile più lento non può essere raggiunto da uno più rapido; giacché quello che segue deve arrivare al punto che occupava quello che è seguito e dove questo non è più (quando il secondo arriva); in tal modo il primo conserva sempre un vantaggio sul secondo“.

Mentre la descrizione più famosa la dobbiamo allo scrittore argentino Jorge Luis Borge: “Achille, simbolo di rapidità, deve raggiungere la tartaruga, simbolo di lentezza. Achille corre dieci volte più svelto della tartaruga e le concede dieci metri di vantaggio. Achille corre quei dieci metri e la tartaruga percorre un metro; Achille percorre quel metro, la tartaruga percorre un decimetro; Achille percorre quel decimetro, la tartaruga percorre un centimetro; Achille percorre quel centimetro, la tartaruga percorre un millimetro; Achille percorre quel millimetro, la tartaruga percorre un decimo di millimetro, e così via all’infinito; di modo che Achille può correre per sempre senza raggiungerla“.

La confutazione però, arrivò immediatamente dal filosofo Diogene di Sinope che alzandosi in piedi, camminò allo scopo di dimostrare la falsità delle conclusioni di Zenone. Mentre Aristotele sostenne invece che il tempo e lo spazio sono divisibili all’infinito in potenza, ma non sono divisibili all’infinito in atto. infatti una distanza finita può essere infinita nella considerazione mentale ma in concreto si compone di parti finite.