L’ABC della Relatività Generale: le basi, i buchi neri, le onde gravitazionali

La Relatività Generale, una delle opere d’arte della scienza del XX secolo, nonché una delle teorie più temute da chi non la conosce: è davvero così complessa? La risposta è sì e no, perché la sua trattazione completa richiederebbe di addentrarsi in un complesso formalismo matematico, ma ciò non preclude la possibilità di comprendere i suoi assunti base e le loro conseguenze.

Per parlare di Einstein, è necessario parlare di Newton. Newton ha infatti posto le basi per la meccanica classica, e in particolare la sua Legge di Gravitazione Universale è ancora oggi la migliore approssimazione per lo studio del moto della maggior parte dei corpi celesti. Applicando tale legge al moto di Urano, ad esempio, si è notato che per far avvicinare le predizioni teoriche alle osservazioni ci dovesse essere un’altra massa oltre la sua orbita. Quella massa dal 1846 ha il nome di Nettuno, il più lontano dei pianeti noti nel Sistema Solare, e rappresenta una delle conferme più eclatanti della Meccanica Newtoniana. Ma allora a cosa serve allora la Relatività se Newton aveva descritto tutto così bene?

I problemi insorgono quando tentiamo di usare la meccanica newtoniana per descrivere non i grandi giganti ghiacciati, ma il moto dei corpi più vicini al Sole, e in particolare di Mercurio. Già nel 1845 Le Verrier aveva scovato delle anomalie nel moto di Mercurio: il suo perielio (il punto dell’orbita più vicino al Sole) si trovava ogni secolo qualche frazione di grado più in avanti di quanto previsto tramite le equazioni di Newton. Qualcosa non andava.

Einstein tra il 1907 e il 1915 portò avanti la sua nuova teoria gravitazionale, un vero e proprio terremoto scientifico che nel corso del ‘900 e degli anni 2000 ha ricevuto una lunga serie di conferme sperimentali. La Relatività Generale è ad esempio in grado di risolvere il problema del moto di Mercurio, di predire l’esistenza di buchi neri e onde gravitazionali e di dare significato alla deviazione della traiettoria dei raggi luminosi che passino vicino ad una massa: ma arriviamoci con calma.

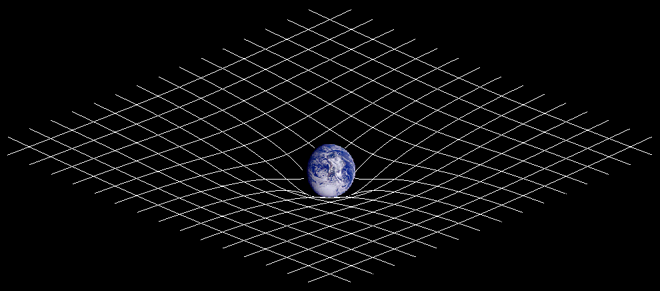
La Relatività Generale è una descrizione geometrica di come si comporta lo spazio-tempo in presenza di una massa (e dell’energia, ma qui ci riferiremo alla sola massa per semplificare la trattazione): lo spazio si curva e il tempo scorre più lentamente. Classicamente per visualizzare questo effetto si utilizza un telo teso al centro del quale sia posta una massa. Il telo naturalmente si incurva verso l’interno, e mettendo una massa più piccola in rotazione sulla curvatura, questa tende ad orbitare attorno alla massa centrale (provare per credere). Questo semplice esempio è molto utile per dare una mano all’intuizione, ma è bene ricordare che deve essere trasposto nelle molto meno intuitive tre dimensioni spaziali e una temporale (lo spazio-tempo appunto) per avere significato fisico. Nella Teoria di Einstein, allora, i corpi in orbita non fanno altro che seguire la curvatura imposta dalla massa centrale e la gravità da forza è ridotta ad un mero effetto geometrico. Inoltre, la curvatura coinvolge anche il tempo, che scorre più lentamente in presenza di massa rispetto al solo spazio vuoto.

Il Principio d’Equivalenza

Il Principio di Equivalenza si può postulare nel modo seguente: “in un campo gravitazionale, si può sempre scegliere un sistema di riferimento in cui le leggi della fisica sono le stesse che si avrebbero in assenza di gravità“. Un esempio classico che viene fatto per spiegare questa affermazione è quello dell’ascensore: se un uomo si trova in un ascensore chiuso nello spazio, non ha modo di sapere se la forza che percepisce è dovuta ad attrazione gravitazionale o ad una forza esterna che agisce sull’ascensore. In altri termini, se foste chiusi in un ascensore accelerato da una forza, tutti i fenomeni che osservereste sarebbero indistinguibili da da quelli che si avrebbero se questo fosse posto in quiete ma in un campo gravitazionale: se faceste cadere un oggetto cadrebbe sul pavimento dell’ascensore, se faceste delle flessioni fatichereste allo stesso modo.

Numericamente, questo principio si traduce nell’uguaglianza tra la massa detta inerziale (quella che determina quanto un corpo viene accelerato in seguito all’applicazione di una forza) e la massa gravitazionale (quella che determina l’attrazione gravitazionale esercitata e subita). Proprio grazie a questa equivalenza tutti i corpi sulla Terra cadono con la stessa velocità come nel famoso esperimento di Galilei dalla Torre di pisa. Se non valesse questa equivalenza, la velocità con cui i corpi cadono dipenderebbe dalla loro massa gravitazionale, e ci sarebbe quindi un modo per distinguere l’effetto dell’attrazione gravitazionale rispetto a quello di una forza esterna, anche ad ascensore chiuso.

Questo principio ha conseguenze enormi, e si applica alla sola forza di gravità, che può essere quindi dimenticata se ci mettiamo in determinati sistemi di riferimento. Meglio ancora, possiamo non trattarla come forza se consideriamo che i suoi effetti siano solamente frutto della geometria dello spazio-tempo, deformata dalla presenza delle masse.

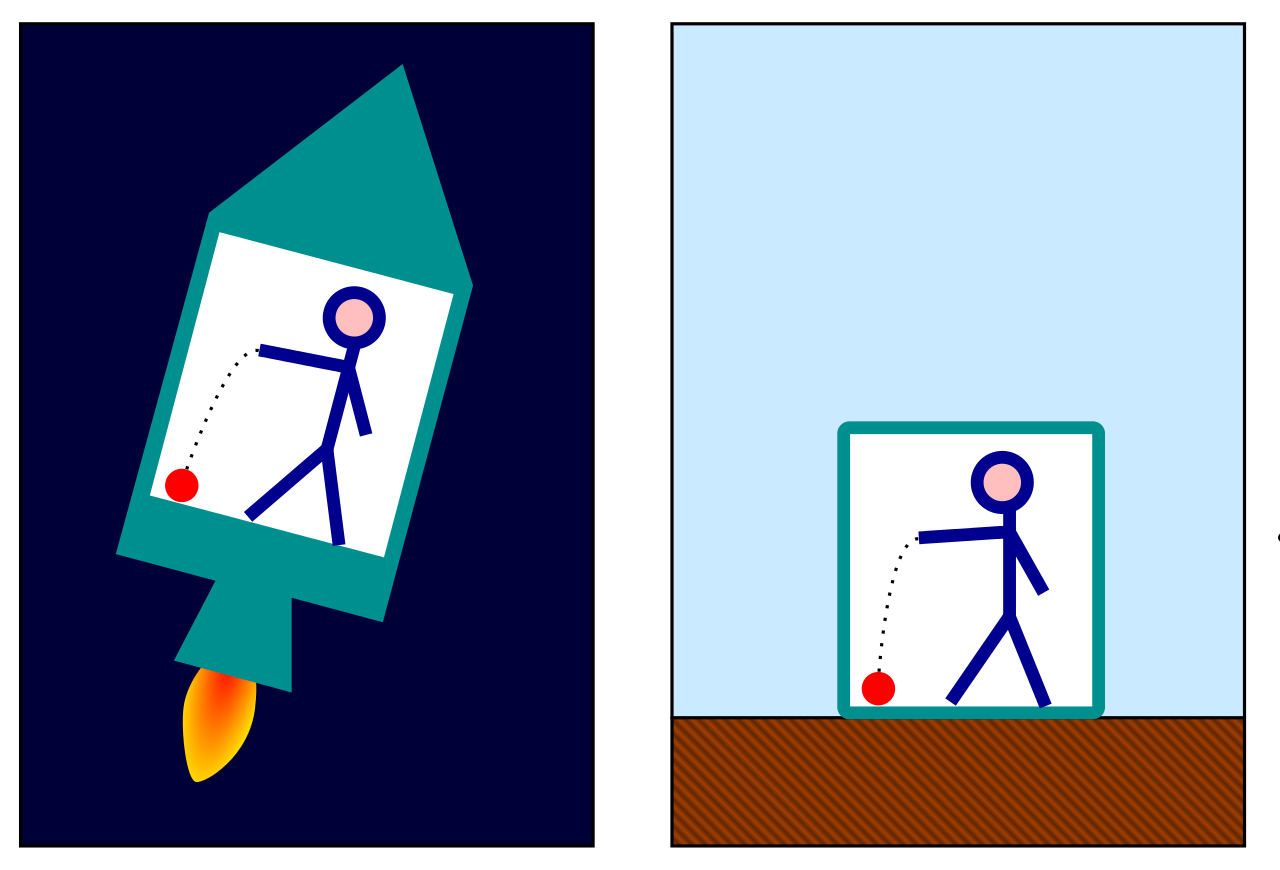
Due esperimenti mentali possono venirci in aiuto per capire un po’ meglio le conseguenze di questo Principio.

La deviazione della luce

Prendiamo il nostro ascensore, e immaginiamolo appeso ad un cavo nel campo gravitazionale terrestre. Sganciamolo nello stesso istante in cui viene lanciato un fotone al suo interno in direzione orizzontale. Grazie al Principio di Equivalenza, dall’interno dell’ascensore vedremo il fotone muoversi in linea retta orizzontale, in quanto l’ascensore in caduta libera è equivalente ad un ascensore in quiete in assenza di gravità, situazione in cui il fotone viaggerebbe orizzontalmente. Un osservatore che invece assiste alla scena da terra (e che fosse in grado di vedere attraverso l’ascensore), noterebbe che la traiettoria del fotone si incurva verso il basso così da restare sempre allo stesso livello dell’ascensore in caduta. La traiettoria curva è il tragitto più breve che il fotone può percorrere nello spazio-tempo deformato dalla Terra, e questa traiettoria è detta geodetica.

Redshift gravitazionale e dilatazione del tempo

Stessa situazione di prima: un ascensore sospeso. In questo caso, sganciamo l’ascensore nel momento in cui un fotone viene lanciato verso l’alto, dal pavimento al soffito. Se misuriamo la frequenza della luce una volta che questa sia giunta sul soffitto, questa sarà invariata se la misura avviene dall’interno dell’ascensore in caduta libera, in quanto per il Principio di Equivalenza osserviamo il moto come se fossimo in assenza di gravità. Un osservatore esterno che misuri la frequenza del fotone al soffitto si aspetterebbe che questa sia aumentata per effetto Doppler rispetto alla frequenza con cui il fotone era partito dal pavimento, così come fa la sirena dell’ambulanza quando si avvicina. Tuttavia questo blueshift (aumento di frequenza) non si osserva, e pertanto ci deve essere un effetto contrario che lo compensa, riducendo la frequenza nella stessa misura in cui questa aumenta per effetto Doppler. Tale fenomeno prende il nome di redshift gravitazionale e quantifica la riduzione di frequenza che si ha nel momento in cui il fotone si allontana dal campo gravitazionale.

L’origine di questo redshift gravitazionale è strettamente legata alla dilatazione del tempo quando ci si allontana dalla massa. Il tempo scorre infatti più lentamente più la massa deforma lo spazio-tempo circostante, e quindi se la luce si allontana dalla massa, oscillerà sempre più lentamente, dando origine al redshift.

Le equazioni di campo di Einstein

Einstein formalizzò tutti questi risultati in alcune equazioni la cui soluzione descrive la curvatura dello spazio-tempo data una massa. Tali equazioni sono dette equazioni di campo e si possono scrivere in forma compatta in questo modo:

Entrare nei meandri matematici delle equazioni di campo ci porterebbe ben oltre gli scopi di questo approfondimento, ma ci basti sapere che sulla sinistra abbiamo degli elementi che descrivono la curvatura dello spazio-tempo e sulla destra abbiamo un elemento che descrive la distribuzione di massa ed energia. Curvatura dello spazio-tempo e massa-energia risultano così indissolubilmente legate, e al variare di una, varia anche l’altra. Le soluzioni delle equazioni di campo forniscono la cosiddetta metrica dello spazio-tempo, un’indicazione della sua struttura e quindi del moto dei corpi che vi si muovono.

Quei simboli in apparenza semplici racchiudono però una grande complessità, e le equazioni di campo non possono essere risolte se non in maniera approssimata e solamente per alcuni casi molto particolari. Per esempio non esistono soluzioni esatte per una coppia di masse (come un sistema stellare binario), mentre esistono soluzioni per alcune tipologie degli oggetti astrofisici più famosi nella cultura popolare: i Buchi Neri.

La soluzione di Schwarzschild

Una delle poche soluzioni esatte che si possono ottenere è quella del caso di una singola massa sferica, non rotante e priva di carica elettrica. Questa è nota come Soluzione di Schwarzschild e vale per lo studio dello spazio-tempo all’esterno di questa massa. I corpi generalmente ruotano, non sono perfettamente sferici e spesso sono carichi: bisogna quindi mantenere bene a mente che tale soluzione è un’approssimazione delle realtà. Eppure, nonostante questo, l’approssimazione è sufficientemente buona da essere utile in molti casi di interesse pratico. Un esempio su tutti? Predice molto bene la problematica orbita di Mercurio. La Soluzione di Schwarzschild descrive inoltre in maniera piuttosto buona la dilatazione del tempo e il redshift gravitazionale.

Un caso particolarmente interessante che deriva dalla Soluzione di Schwarzschild è quello dei buchi neri. Un buco nero è dato da una massa così compatta da essere considerabile come concentrata in un singolo punto, come nel caso dei residui massicci delle supernovae. In tale situazione lo spazio-tempo è talmente incurvato che i fotoni che vi si trovano sono costretti a rimanervi intrappolati: non esistono infatti traiettorie (geodetiche) che i fotoni possano percorrere per uscire dal Buco Nero. Per questo i buchi sono neri, perché la luce vi resta intrappolata. Questo intrappolamento avviene entro una distanza dal punto centrale detta raggio di Schwarzschild e il confine sferico delimitato da questo raggio è detto orizzonte degli eventi. Un osservatore che attraversi questo orizzonte, ammettendo che non venga distrutto dalle enormi forze in gioco, non noterebbe alcuna differenza rispetto al suo viaggio precedente. Un osservatore esterno che lo guardi da lontano lo vedrebbe invece avvicinarsi all’infinito all’orizzonte, senza mai arrivarci, come diretta conseguenza della dilatazione dei tempi in presenza di massa.

Onde gravitazionali

Muovendo una mano sul pelo dell’acqua si formano delle onde. Allo stesso modo, accelerando una massa e perturbando quindi la deformazione nello spazio-tempo che essa genera, in questa si originano delle increspature che prendono il nome di onde gravitazionali. Si tratta di segnali debolissimi, anche nel caso in cui vengano generati da enormi accelerazioni di massa come quelle dei buchi neri in rotazione (noti come Buchi Neri di Kerr, che sono il risultato di una delle poche altre soluzioni delle equazioni di Einstein). Quando queste onde si propagano nello spazio, lo deformano, facendolo allungare e contrarre ritmicamente. Sorge spontaneo chiedersi come sia possibile misurare questi eventi, dato che sia noi che i nostri strumenti di misura ci dilatiamo o accorciamo tanto quanto lo spazio stesso. Eppure un modo c’è, ed è quello sfruttato dai rivelatori di onde gravitazionali come LIGO e Virgo: la luce impiega più tempo ad attraversare uno spazio allungato e meno ad attraversarne uno contratto. Prendendo due condotti uguali, tra loro perpendicolari e di cui uno dei due si trovi nella direzione da cui proviene l’onda, possiamo quindi misurare il tempo che la luce impiega ad attraversarli. Se i tempi non coincidono, significa che uno dei due è contratto rispetto all’altro e quindi ha subito il passaggio dell’onda gravitazionale.

Con Einstein la nostra visione dell’Universo è cambiata. Andando dai problemi locali, come i buchi neri, a quelli universali, le equazioni di campo hanno permesso di elaborare veri e propri modelli cosmologici. L’evoluzione dell’universo è infatti diretta conseguenza di quanta massa vi si trovi, di come sia distribuita e di quali siano i suoi effetti sullo spazio-tempo: elementi legati insieme dalla Teoria di Einstein.

Sebbene la storia dell’astrofisica non inizi con Einstein, con la sua Teoria della Relatività Generale è nato qualcosa di nuovo rispetto ai secoli che la hanno preceduta. Einstein ha infatti apportato dei cambiamenti alla nostra comprensione dell’Universo, della sua evoluzione e dell’evoluzione degli oggetti che lo popolano, cambiamenti dalla portata rivoluzionaria che ancora oggi, a distanza di oltre un secolo, hanno in serbo molte sorprese.

Fonti:
V. Ferrari, Lecture Notes on General Relativity, Black Holes and Gravitational Waves (2018)
L. Carroll, An Introduction to Modern Astrophysics (2017)