Vento Solare – Come lo scoprì Parker?
Il Fisico Eugene Parker predisse il vento solare come diretta conseguenza dell’impossibilità di elaborare un modello di atmosfera del Sole simile a quello elaborato per la Terra. Vediamo insieme i passaggi che hanno portato alla scoperta del Vento Solare grazie all’aiuto della fisica e di un po’ di matematica, ponendo attenzione all’evoluzione del pensiero dietro il modello fisico.
Premessa:
Per capire meglio, partiamo dal definire un primo modello approssimativo per l’atmosfera terrestre, lo stesso che si è cercato di applicare inizialmente al Sole senza successo. L’atmosfera è un sistema legato. Significa che la sua dinamica dipende dall’azione di un campo di forze: il campo gravitazionale terrestre.
Per elaborare un modello è importante introdurre delle ipotesi. Ci permettono di introdurre delle semplificazioni, perdendo però un po’ di generalità, ovvero il modello sarà applicabile a meno casi. Infatti affinché un modello sia il più fedele possibile bisogna introdurre il minor numero di ipotesi. Come abbiamo visto per il campo gravitazionale della Luna, spesso è preferibile cominciare ad elaborare inizialmente un modello più semplice e successivamente cominciare a togliere gradualmente le ipotesi. Infatti questo che stiamo per vedere è considerabile un primo modello da cui deriva quello dell’Atmosfera Standard. Vediamo le ipotesi che introducono le semplificazioni necessarie.
Le Ipotesi del Modello Terrestre.
- L’ipotesi di atmosfera sottile, permette di elaborare un modello dell’atmosfera in cui la gravità é considerabile costante ed approssimabile con il suo valore al suolo g0. Ciò è ammissibile perché la maggior parte dell’atmosfera terrestre è confinata in pochi chilometri dal suolo.
- Anche l’ipotesi di atmosfera isoterma (alla stessa temperatura) è accettabile. Infatti nonostante la temperatura decresca in troposfera salendo di altitudine con una variazione di 6 K/km, comunque negli strati più densi raggiunge una temperatura che non si discosta molto dal valore medio (288 K).
- L’ipotesi di atmosfera isostatica impone che sia un’atmosfera senza venti. Infatti, ricordiamo, è un primo modello approssimativo globale.
La condizione di isostaticità mette in relazione l’azione delle forze e delle energie in gioco con la dinamica del fluido. Essendo isostatica, il fluido rimarrà in equilibrio (fermo e non soggetto ad accelerazioni) perché l’azione delle forze si controbilancerà. Il fluido viene descritto dall’equazione di Navier Stokes, che a causa di queste ipotesi vengono notevolmente semplificate, rendendo il problema determinato univocamente dal bilancio fra l’energia termica, agente attraverso la variazione di pressione rispetto l’altitudine, e l’azione dell’energia potenziale gravitazionale. Ciò permette di giungere alla legge che descrive l’andamento esponenziale della pressione (P) rispetto l’altitudine (z):
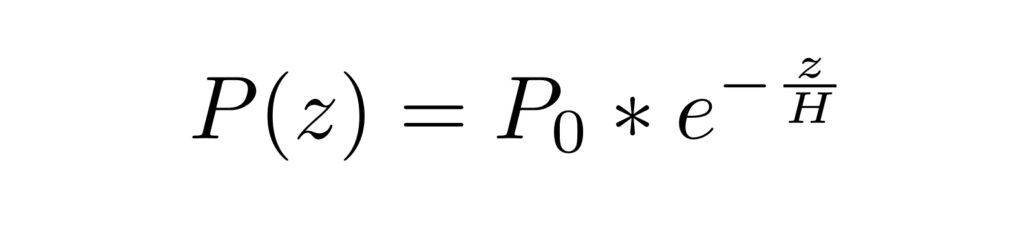
Dove H è chiamata Altezza di Scala, una grandezza che determina quanto velocemente l’esponenziale tende a zero. P0 indica la pressione al suolo, ed e è il numero di Nepero. Nei dettagli l’evoluzione del ragionamento.

Abbiamo già parlato dell’altezza di scala per ricavare la velocità di rotazione delle pale dell’elicottero marziano Ingenuity in questo articolo: Ci vuole Ingegnosità per Volare su Marte.
Applicare lo stesso modello all’Atmosfera Solare.
Cercando di applicare lo stesso modello all’atmosfera solare ci rendiamo conto subito che non possiamo considerare tutte le stesse ipotesi fatte per la Terra. Infatti, l’atmosfera del Sole non è un’atmosfera sottile. Di conseguenza non possiamo usare la semplificazione per cui l’accelerazione gravitazionale sia approssimabile al valore alla superficie. Ciò ci costringe a dover usare la legge di gravitazione universale nel bilancio. Permane l’ipotesi di atmosfera isoterma. Si giunge ad una relazione simile che descrive l’andamento esponenziale della pressione rispetto alla distanza dal Sole.
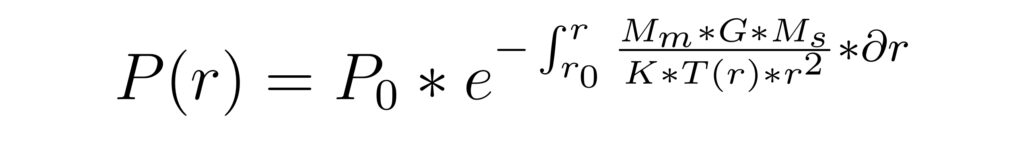
Dove all’esponenziale ritroviamo una funzione integrale che risolta, porta ad un valore finito della pressione ad una distanza infinita, cosa che non ha senso fisico. Infatti affinché lo sia, è necessario che per distanze che tendono ad infinito [r→∞] la pressione sia zero [P(∞) = 0]. In altre parole, la funzione integrale rappresenta una Altezza di Scala H che, al contrario del modello terrestre, varia con la distanza r. E’ necessario che per distanze che tendono ad infinito [r→∞], tenda anche lei ad infinito [H→∞]. Fra i dettagli è espresso il ragionamento che porta al risultato:

Nuove Ipotesi per l’Atmosfera Solare
Affinché possa convergere a zero, bisogna abbandonare l’ipotesi di atmosfera isoterma e considerare una Temperatura che varia con la distanza [T(r)]. Quindi la temperatura dell’atmosfera solare dovrebbe tendere a zero con un ritmo più veloce del quadrato della distanza r2 affinché l’integrale diverga ad infinito. Ciò farebbe tendere la funzione P(r) a zero come ci aspettiamo.
Comunque, un’atmosfera statica e non isoterma non ha molto senso fisico. Infatti si genererebbero fenomeni di trasporto dovuti alla differenza di temperatura. Quindi cadrebbe anche l’ipotesi di atmosfera statica. Qui entra in gioco la Teoria di Parker.
La Teora di Parker sul Vento Solare:
Cos’è il Vento Solare e Perché si forma.
Il Vento Solare nasce dalla cromosfera. E’ un plasma di protoni ed elettroni che si allontana ad una velocità acquisita riscaldandosi da qualche decina di migliaia di gradi ad oltre 2 milioni di gradi. L’intenso riscaldamento è dovuto ai moti convettivi negli strati più interni del Sole e sia alla dinamica complessa dovuta ai campi magnetici solari in prossimità della sua superficie che veicolano il plasma. Al contrario di quanto sia più intuitivo, la velocità non è ne costante e nemmeno diminuisce con l’allontanarsi dal Sole, bensì aumenta fino a diventare supersonica a qualche raggio solare di distanza dal Sole.
Un comportamento per certi versi simile a quello di un fluido in un ugello convergente-divergente di un razzo. In un ugello del genere, la velocità del fluido aumenta passando per la condizione di strozzamento nella sezione di gola (dove la velocità del fluido diventa transonica), e prosegue espandendosi nel divergente a velocità supersoniche, convertendo l’energia termica del fluido in energia cinetica.
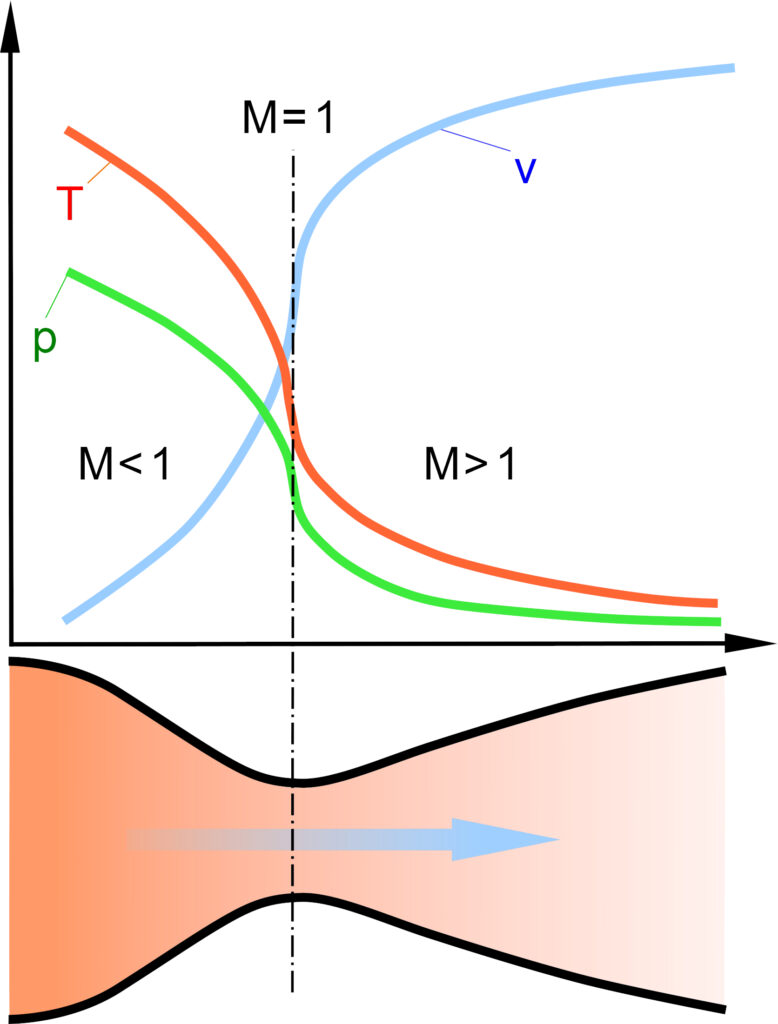
Un’Atmosfera Dinamica per il Sole: Il Vento Solare.
Parker elimina l’ipotesi di atmosfera statica, ma introduce quella di flusso stazionario. Il vento solare viene dunque descritto dalle Equazioni di Navier Stokes come un fluido che si muove a velocità costante rispetto al tempo ma che varia solo rispetto alla distanza dal Sole. Attraverso l’introduzione della velocità del suono [Cs] per il vento solare, Parker lega la velocità alle proprietà termodinamiche di questo fluido, che viene trattato come un gas molto rarefatto. Questo parametro è molto importante perché il vento solare è un flusso supersonico. Attraverso questa trattazione si giunge ad una relazione chiamata funzione H(r), che lega la velocità del Vento Solare alla distanza dal Sole, e che deve valere zero quando la velocità del fluido diventa transonica. Fra i dettagli, i dettagli del calcolo.

La funzione H(r) assume come soluzione non un numero, ma una famiglia di funzioni, ovvero funzioni che assumono caratteristiche simili fra loro, che descrivono (in questo caso) la velocità rispetto alla distanza [v(r)] attraverso le condizioni imposte dalla funzione H(r). Funzioni di questo tipo sono chiamate funzioni differenziali. Mentre le soluzioni possono esistere tutte a livello matematico, solo alcune hanno un reale significato fisico e fra queste solo una è la descrizione del fenomeno fisico che stiamo studiando.
Tante descrizioni per il Vento Solare. Una sola possibile
La funzione che descrive il vento solare è proprio la soluzione indicata come “V” nel grafico sottostante. Una funzione strettamente crescente che parte da un valore di velocità iniziale subsonica, passa nel punto dove la funzione H(r) si annulla (detto punto critico, in cui la velocità del vento solare eguaglia la velocità del suono [Cs], situato ad una raggio solare), ed aumenta con l’aumentare della distanza a velocità supersoniche.
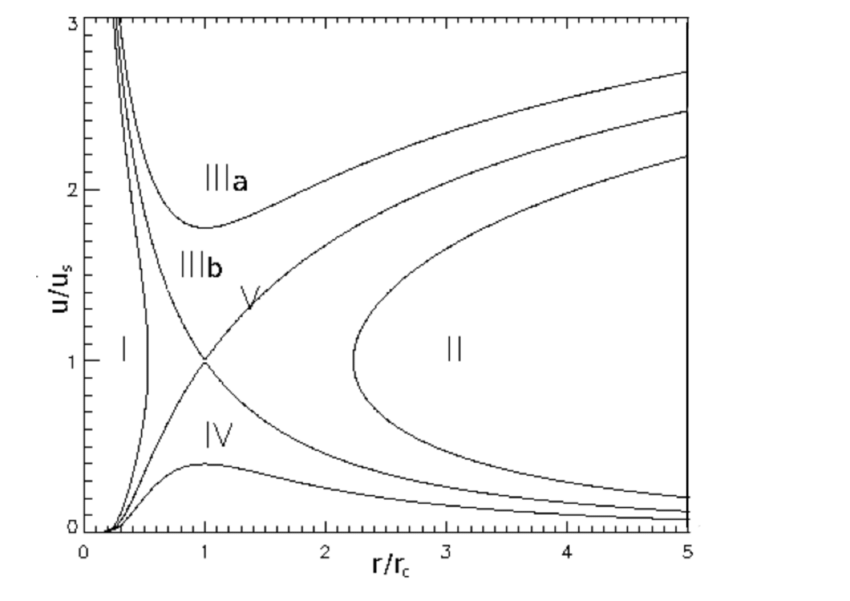
La I non ha significato fisico perché a parità di distanza si hanno due soluzioni, una subsonica ed una supersonica.
La II non ha significato fisico per lo stesso motivo, inoltre non incontra mai la Corona Solare (da cui ha origine il vento solare).
La IIIa descrive un flusso che dalla Corona si allontana a velocità supersonica e decresce fino ad un minimo in corrispondenza di una distanza di un raggio solare, ed a distanze maggiori aumenta.
La IIIb descrive un flusso che dalla Corona si allontana a regime supersonico, ed a distanze superiori di un raggio solare passa in regime subsonico, che tende a zero all’infinito.
La IV descrive un flusso che nasce nella Corona e la cui velocità aumenta fino ad una distanza di un raggio solare e poi diminuisce. Questa soluzione è chiamata brezza solare.
La V è proprio la funzione che descrive il Vento Solare per come lo conosciamo.
Credits: ResearchGate
La Scoperta del Vento Solare
La sonda sovietica Luna 1, che lanciata con successo nel 1959 e diretta verso la Luna, passando oltre le Fasce di Van Allen, osservò la presenza di particelle cariche ad alta energia, scoprendo così il Vento Solare. Altre misurazioni furono seguite dalla sonda Luna 2 e dalla Mariner 2, una delle missioni Mariner non destinate a Marte, bensì a Venere, lanciata nel 1962. Le misurazioni confermarono quanto predetto dalla Teoria di Parker anni prima. Dunque Parker predisse il Vento Solare ben prima che fu realmente osservato.

Il Vento Solare e la Terra
Il Vento Solare investe la Terra con una velocità media di circa 400 km/s, con una densità media di circa 5-8 ioni (ed elettroni)/cm3. Quando incontra il campo magnetico terrestre genera un’onda d’urto .Questa interazione lo frena, facendolo passare da una velocità supersonica ad una subsonica. Il vento solare inoltre è così caldo che congela al suo interno le linee di campo magnetico solare. Si tratta del comportamento di un plasma molto simile a quello che può avvenire all’interno di un materiale superconduttore che presenta delle impurità.
Ciò gli permette di interagire magneticamente con il campo magnetico terrestre, dando vita a dei fenomeni di disconnessione e riconnessione magnetica, popolando di particelle le Fasce di Van Allen. Queste ultime le abbiamo trattate nell’approfondimento che vi riportiamo sottostante.
Venti solari più intensi, come quelli prodotti da brillamenti ed espulsioni di masse coronale [CME], se dirette verso la Terra possono causare anche fenomeni come tempeste geomagnetiche. Vedremo in dettaglio la dinamica di un plasma in un altro articolo (troverete il link qui quando sarà pubblicato).
Altre informazioni sul Vento Solare potete trovarle in questo precedente articolo:
In Copertina: Foto di Eugene Parker con una foto del Vento Solare nel 1977. Fonte: The New York Times
[EDIT: 10-01-2023]

