Analisi dei dati topologica: un ponte tra la geometria e l’analisi dei dati
Oggi parliamo di un nuovo approccio geometrico all’analisi dei dati: l’analisi dei dati topologica.
L’intuizione al centro dell’analisi dei dati topologica è cercare di sfruttare gli strumenti della topologia algebrica (una branca della matematica) per studiare le proprietà di insiemi formati da un elevato numero di dati derivanti da sorgenti più e meno comuni, con diversi gradi di informazione e rumore.

Che cosa è la topologia algebrica? Essendo una delle branche più importanti e vaste della matematica, non è facile dare una risposta completa in poche righe, ma il concetto alla base della materia è molto naturale: di fronte al problema di determinare in maniera sistematica le proprietà importanti ed essenziali di uno spazio (topologico, e.g. si pensi a qualsiasi oggetto geometrico), i matematici si sono trovati di fronte al problema che la geometria può essere estremamente complicata e di rado fornisce metodologie per studiare i propri oggetti. D’altra parte l’algebra (una delle branche più antiche della matematica), risulta più adatta a permettere studi sistematici dei propri oggetti ed è qui che nasce la topologia algebrica: cercare di studiare gli oggetti topologici attraverso metodi algebrici. (Si potrebbe comunque argomentare, e a ragione, che l’algebra non è essenzialmente diversa della geometria, a dirla tutta si potrebbe anche argomentare che sotto molti aspetti algebra e geometria non siano in realtà distinguibili, così come il resto della matematica. In questo senso è importante sottolineare che il vantaggio di studiare oggetti geometrici grazie all’algebra non deriva da una reale asimmetria della matematica, quanto più ad un’asimmetria con cui determinati oggetti sono stati introdotti).
Come abbiamo già introdotto nell’articolo su Escher e Penrose (https://wp.me/p7V5i9-2fm), uno degli aspetti più importanti in topologia algebrica è l’assegnazione di invarianti che racchiudano alcune delle proprietà geometriche di un certo spazio. Noi avevamo raccontato, in quell’articolo, di una coomologia, ma ci sono moltissimi altri tipi di invarianti, molti dei quali di origine (co)omologica.
Un primo aspetto importante che si vuole sapere riguardo uno spazio è l’eventuale presenza di “buchi”, questo problema semplice è estremamente importante ed estremamente ragionevole: due spazi che hanno diversi tipi di buchi sono necessariamente diversi tra loro e quindi li possiamo distinguere con certezza, sono spazi diversi. La presenza o meno di eventuali buchi in uno spazio è misurata dall’omologia di quello spazio: spazi che hanno diverse omologie sono, appunto, diversi. Purtroppo: spazi con stessa omologia non sono necessariamente equivalenti, e questo è uno dei limiti della topologia algebrica, ovvero trovare un invariante che sappia perfettamente distinguere quando due spazi siano essenzialmente uguali o diversi.
Si pensi ad esempio ad una sfera e ad una circonferenza, ad una ciambella e ad una tazza per il caffè, quali di questi spazi sono certamente diversi per il tipo di buchi?
Veniamo ora all’analisi dei dati topologica: grandi moli di dati sono spesso difficili da analizzare con precisione, ma l’intuizione geometrica qui ci viene incontro. Questi dati possono essere analizzati in primo approccio proprio grazie agli strumenti della topologia algebrica, cercando quindi di estrarre informazioni su come questi dati siano legati tra loro e quali informazioni globali possiamo trarre da questi: in questo campo l’invariante principale è chiamato, per l’appunto, omologia persistente. Il termine persistente qui si riferisce al fatto che le informazioni “interessanti” sono quelle che rimangono più a lungo quando studiamo una nube di dati a risoluzioni diverse.
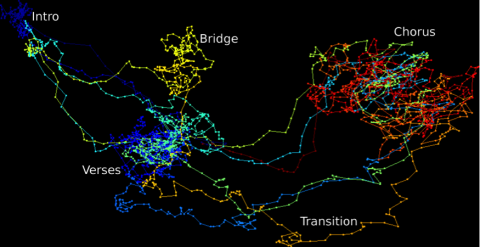
Credits: Duke University
L’importanza di questo nuovo approccio è sia pratica che storica: è infatti uno dei primi esempi in cui strumenti avanzati della topologia algebrica vengano implementati in un ambito applicativo in maniera non solo funzionale, ma anche caratterizzante di un nuovo possibile modo di pensare un certo problema.